问题:用二分法求f(x) = 0的根。

首先我们先知道二分法的定义：
对于区间[a，b]上连续不断且f（a）·f（b）<0的函数y=f（x），通过不断地把函数f（x）的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫二分法。

算法描述
算法:(二分法)
(1)计算f(a), f(b),若f(a)f(b)>0 ,则算法失效,停止计算
(2)令x=（a+ b）/2,计算f(x)
(3)若|f(x)|<ε或|b-a|<ε,停止计算,输出近似解x
(4)若f(a)*f(x)<0,则令b=x;否则令a=x
(5)返回第2步
源程序代码及运行结果截图

#include<iostream>
using namespace std;
/*
@to do:获取自变量x的函数值
@param x:自变量x
*/
float getBinarySearchFuntion(float x) 
{
	return x * x - 3*x + 2.0f;
}
/*
@to do:获取误区范围小于e的获取区间[a,b]的根
@param a:开始查找的下限
@param b:开始查找的上限
@param e:精确度，便于跳出循环
*/
float getSearchAnser(float a,float b,float e) 
{
	if (getBinarySearchFuntion(a)*getBinarySearchFuntion(b)>0)
	{
		//查找算法失效
		return 0.0f ;
	}
	
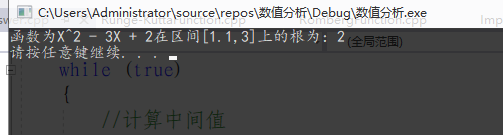
	while (true)
	{
		//计算中间值
		float x = 0.5f*(a + b);
		//获取函数值的绝对值
		float f = abs(getBinarySearchFuntion(x));
		float tol = abs(b - a);
		//判断是否跳出循环
		if (f < e || tol < e)
		{

			return x;
		}
		//开始折半搜索查找
		if (getBinarySearchFuntion(x)*getBinarySearchFuntion(a) < 0)
		{
			b = x;
		}
		else
		{
			a = x;
		}
	}
	
}
int main()
{
	//测试数据
	float a = 1.1f;
	float b = 3.0f;
	float e = 1e-8;
  float x=	getSearchAnser(a, b, e);
  cout << "函数为X^2 - 3X + 2在区间[" << a << "," << b << "]" << "上的根为：" << x << endl;
	system("pause");
	return 0;
}