1. 简介

        深度优先搜索（DFS）：对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。
举例：

        上图是一个无向图，如果从A点发起深度优先搜索(以下的访问次序并不是唯一的，第二个点既可以是B也可以是C,D)，则我们可能得到如下的一个访问过程:A->B->E(没有路了!回溯到A)->C->F->H->G->D(没有路，最终回溯到A,A也没有未访问的相邻节点，本次搜索结束)

深度优先遍历图的方法是，从图中某顶点v出发：

• (1) 访问顶点v；
• (2) 依次从v的未被访问的邻接点出发，对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问；
• (3) 若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

---

        广度优先搜索算法(BFS，又称 宽度优先搜索)是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。

• (1) 访问顶点v；
• (2) 访问v的未被访问的所有邻接点；
• (3) 从V的所有领接点出发，访问所有的领接点；
• (4) 重复以上操作，直到图中所有顶点均被访问过为止。

下面举个例子：
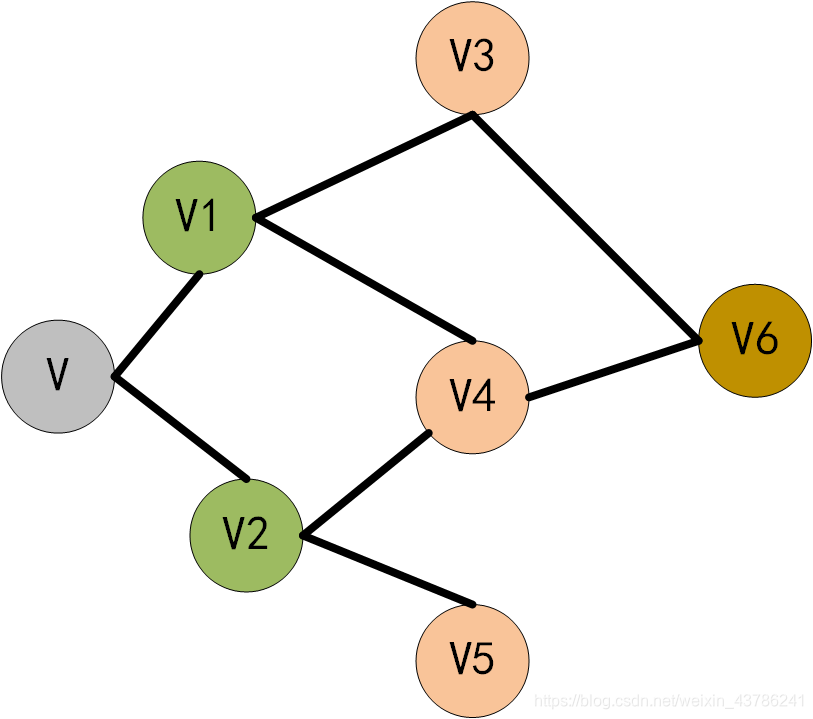
下图为一个无向图，从V出发，广度遍历整个无向图：

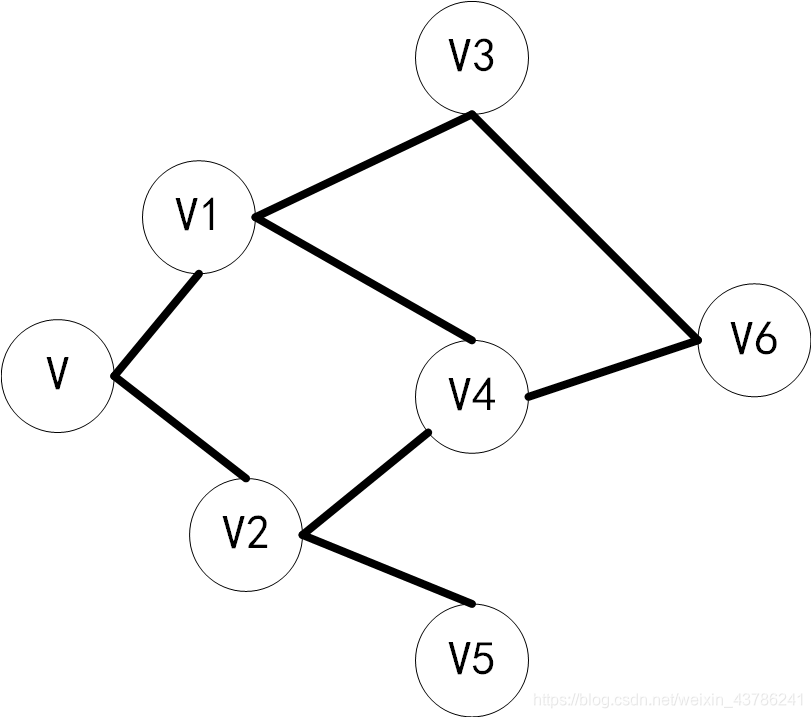
先访问顶点V：

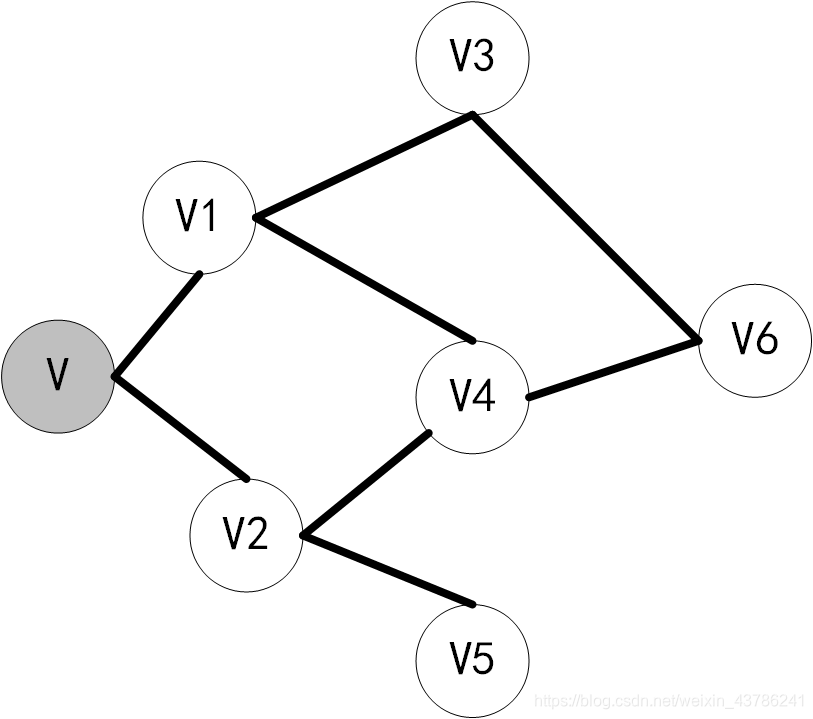
再访问V的领接点V1、V2

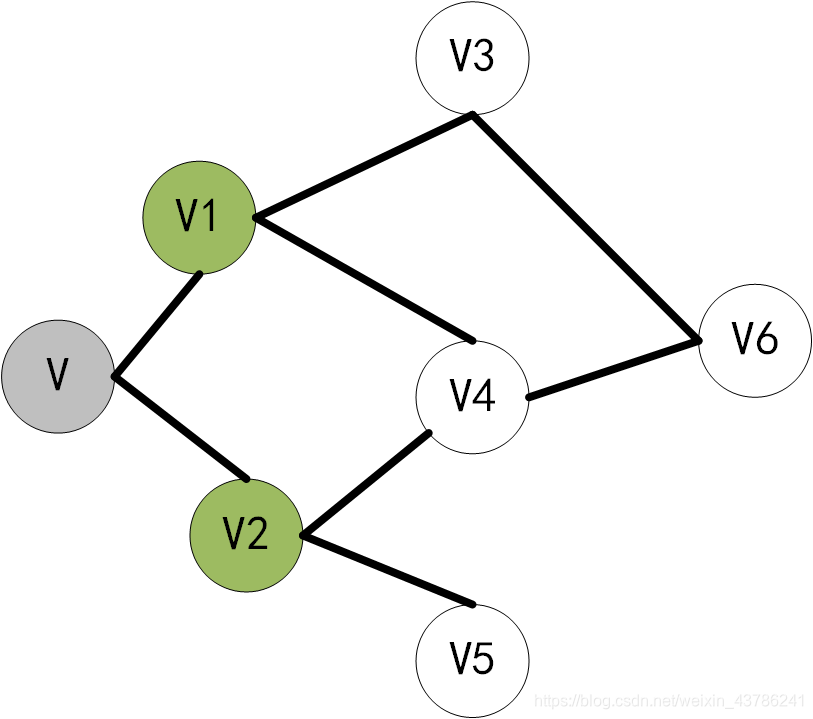
然后访问V1、V2的领接点V3、V4、V5

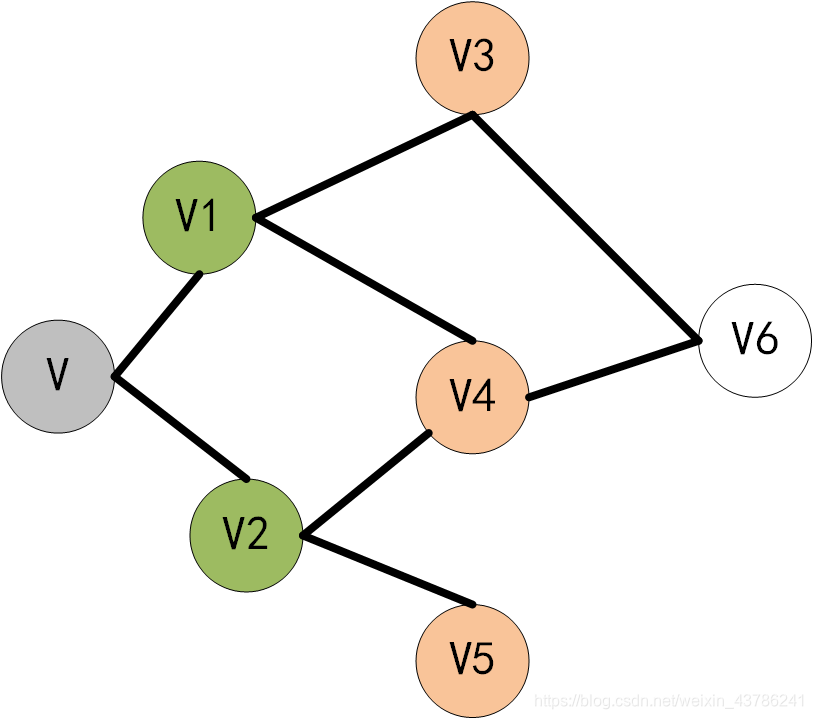
最后访问V3、V4的领接点V6

2. python举例

        LeetCode104. 二叉树的最大深度
        给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。说明: 叶子节点是指没有子节点的节点。
        示例：
        给定二叉树 [3,9,20,null,null,15,7]，

        返回它的最大深度 3 。

1. DFS

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None:return 0
        else:
            l = self.maxDepth(root.left)
            r = self.maxDepth(root.right)
            return max(l, r)+1

3. BFS

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None:return 0
        else:
            from collections import deque
            depth = 0
            queue = deque([root])
            while queue:
                depth += 1
                layer_nood = []
                while queue:
                    root = queue.popleft()
                    if root.left:layer_nood.append(root.left)
                    if root.right:layer_nood.append(root.right)
                queue = deque(layer_nood)
            return depth