路径优化搜素算法

日期： 2018-11-26 分类：跨站数据测试 312次阅读

一.深度优先搜索算法(DFS)

1.算法介绍

https://zh.wikipedia.org/wiki/深度优先搜索

DFS（Depth-First-Search）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
一般使用栈(占内存)的数据结构实现。

2.算法步骤

1.访问顶点v
2.依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问
3.若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

3.举例

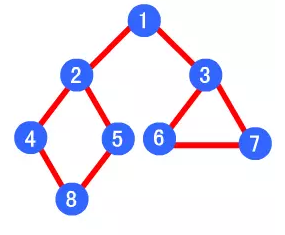
DFS 在访问图中某一起始顶点 v 后，由 v 出发，访问它的任一邻接顶点 w1；再从 w1 出发，访问与 w1邻接但还没有访问过的顶点 w2；然后再从 w2 出发，进行类似的访问，… 如此进行下去，直至到达所有的邻接顶点都被访问过的顶点 u 为止。
接着，退回一步，退到前一次刚访问过的顶点，看是否还有其它没有被访问的邻接顶点。如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问；如果没有，就再退回一步进行搜索。重复上述过程，直到连通图中所有顶点都被访问过为止。

深度优先遍历顺序为 1->2->4->8->5->3->6->7

二.广度优先搜索(BFS)

1.算法介绍

BFS（Breadth-First-Search）是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。BFS同样属于盲目搜索。
一般使用队列数据结构来实现BFS。

2.步骤

1.首先将根节点放入队列中。
2.从队列中取出第一个节点，并检验它是否为目标。如果找到目标，则结束搜寻并回传结果。否则将它所有尚未检验过的直接子节点加入队列中。
3.若队列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
4.重复步骤2。

3.举例

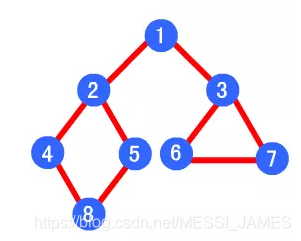
广度优先算法的遍历顺序为：1->2->3->4->5->6->7->8

三. Dijkstra算法

1.算法介绍

Dijkstra(迪杰斯特拉)算法使用了广度优先搜索解决赋权有向图的单源最短路径问题。该算法存在很多变体；Dijkstra的原始版本找到两个顶点之间的最短路径，但是更常见的变体固定了一个顶点作为源节点然后找到该顶点到图中所有其它节点的最短路径，产生一个最短路径树。 Dijkstra是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。注意该算法要求图中不存在负权边。

2.步骤

（1）定义变量：
定义一个数组dist，dist[m]表示顶点s到顶点m的最短距离。（在迭代过程中，里面的值可能不是最终最短距离，但是是当前考虑到已经扫描到的边的最短距离）
定义一个集合T，里面存放着已经查询到最终最短路径的顶点集合。
（2）初始化：
任取顶点 i，如果 s 和 i 直接相连，则dist[i]=W(s,i)，否则 W(s, i) 为无穷大。
T 集合只包含顶点 s。
（3）迭代：
A、从dist中找到最小值（除去集合 T 中包含的点），记为 dist[r]=d，然后将顶点 r 划入到集合 T 中。
B、对于每一个不属于集合 T 的点，比如顶点 q，查看新加入的顶点 r 是否可以直接到达顶点 q，如果是，则比较通过顶点 r 到达顶点 q 的路径长度和当前的dist[q]值，然后取较小值，即 dist[q] := min(dist[r]+W(r, q), dist[q])
C、跳回到步骤A，直到所有的点都进入到了集合 T。
D、dist 中存放的值即为每个点的最终最短路径。