DEA–SBM model

这一篇内容是比较理论的，更多的是探讨模型的性质。

SBM与CCR（从CCR往SBM推）

首先，写出CCR模型：



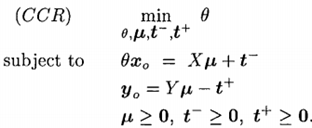
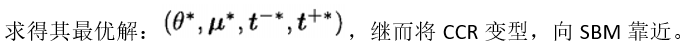
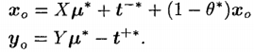
重新定义部分变量：

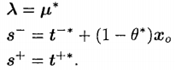
然后把这些带进SBM模型的目标函数中，观察θ与ρ之间的大小：

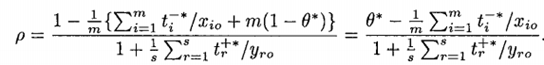
可以很明显得观察到θ≥ρ。

SBM efficiency=CCR efficiency

接下来，证明CCR有效与SBM有效是等价的。

一、 CCR推向SBM：

如果CCR模型是无效的，有两种情况：

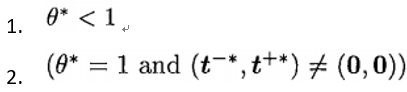
如果是第一种情况，根据上述求得的等式：

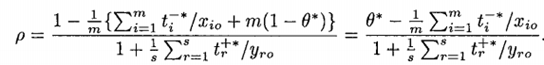
可以知道ρ必定小于1。

那如果是第二种情况，虽然θ=1但是松弛不全为0，同样的根据上述等式，可以得出ρ≤1，即SBM模型无效。

二、 SBM推向CCR：

如果SBM模型是无效的，即松弛变量不全为零，即：

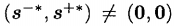
（这里要提及上一篇提及的SBM与CCR效率分数比较大小，从SBM推得CCR部分所涉及的式子：
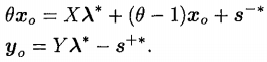以及

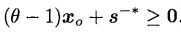
有着两个式子可知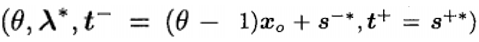：是CCR模型的一个可行解。
那么接下来就θ的值进行分类讨论：

1. 若CCR的解θ=1的，那么
   
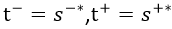
   又上述给出的：
   
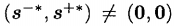
   因此CCR模型的松弛变量t不全为零，CCR模型也是无效。

综上，可以得出，SBM与CCR这两个模型其实是等价的。

Oriented SBM models

这一部分是针对SBM模型进行一个变化。输入导向型的模型保留目标函数中的分子部分，而输出型的则是保留分母部分，并且在约束条件中有所变化。具体看下面模型：

Input-oriented SBM Model

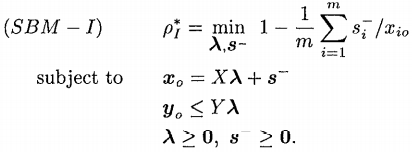
Output-oriented SBM Model

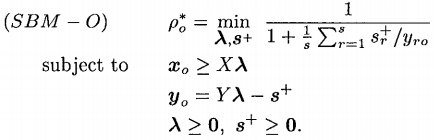
comparison

这个改变过后的模型与原始模型相比，目标函数全部变大：

对于 input-oriented SBM Model来说，目标函数省略了分母部分，原始模型中的分母大于1，那么舍去之后，目标函数变大，即：

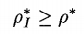
同理，对于Output-Oriented SBM Model来说，它是省略了分子部分，而原始模型的分子是小于1的，舍去之后反而变大，即：

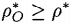
加权SBM模型

这一部分更多的是体现了决策者的倾向。模型具体如下：

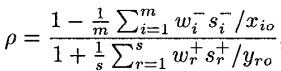
其中对于w有如下限制：

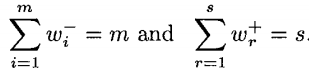
这个权重值w体现了当前决策单元的重要性。并且这个w的计算公式是：

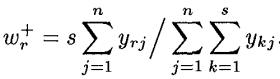
这个是关于输出的，那么对于输入部分的权重亦是如此。

SBM无效率的分解

这块内容是针对SBM模型的目标函数进行展开。首先观察目标函数：

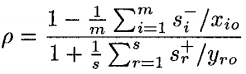
将用新变量进行部分替换：

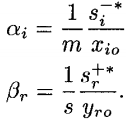
因此得到新的（等价的）目标函数：

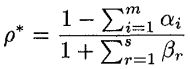
这个分解的意义在于可以准确的直到这个决策单元无效的来源以及无效程度。