DEA–CCR模型

首先，DEA，也就是data envelopment analysis，它是一种运筹学和研究经济生产边界的一种方法，也是一种效率评价的方法。

分式模型

首先对于数据，我们有投入数据X还有输出数据Y。我们给它们附以权重值，给X赋值v，给Y赋值u，要注意的是，这里的u、v是未知的且都是非负值，这样就可以得到虚拟的投入与虚拟的产出。

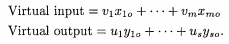
将其进行比值计算。按照常理，输出越大越好，投入越少越好，这样的结构才是最合理的，那么我们就希望这个比值越大越好。

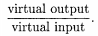
接下来，我们可以对这个比值作出假设，假设它的范围在0到1之间。数据是给定的，即已知的，那些个权重是未知的，我们要做的便是确定这些权重的值，使得目标函数最大，并且对于其他决策单元（DMUs）来说，它们的比值也满足0到1这个假设。分式规划如下（fractional programming）:

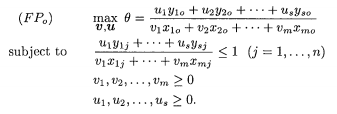
线性模型

分式模型计算时候比较麻烦，因此对其进行变形。
是将上面的分式模型的分母部分令其为t,即：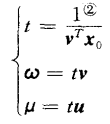
继而进一步变形：

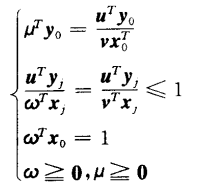
最终得到模型：

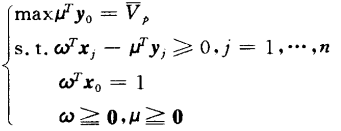
在我上述的图片中，最终线性模型用的权重参数是w、u，但是在很多其他书本上，用的是与分式模型中一样的u,v：

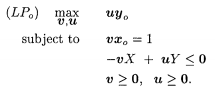
不管用的是什么，只要知道它们的含义其实是不同的！并且这个思想挺重要的，在后续dea学习中也会出现。

对偶模型

有了线性规划模型以后，我们可以运用运筹学线性规划的知识对其变形。目标函数有求max变成求min。具体怎么变化的请自学运筹学。得到对偶模型：

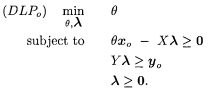
由于限制条件并不是等式，添加松弛变量，得到：

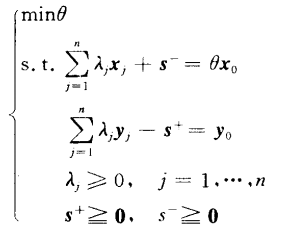
目前我个人学习过程中，对偶模型出现的频率更高一点。比如图片中的这个模型，是基于投入向的。是对所考虑的DMU的投入x0进行一个比例theta倍的压缩之后，再用松弛变量进行微调。又是这个模型是input-oriented，此时的产出y0就只进行微调。反之亦然，如果是基于输出向的模型，就是投入x0进行微调，产出y0经过压缩之后在进行微调。

并且有一个概念，分式模型与线性模型称为乘子型，而对偶模型称为包络型。

DEA有效

接下来讲一下有效的概念。由于分式模型与线性模型是等价的，我们就详细说一下线性模型与对偶模型。对于包络型，也就是对偶型来说，只有目标函数theta为1且所有的松弛变量都是零时，我们才能说这个DMU0是有效的。而对于线性模型来说，若只有目标函数为1这个条件，只能说这个DMU0是弱有效的，其实也就是无效；但是如果既满足目标函数为1并且系数u、v是大于零的，这时候才能说这个DMU0是有效的（强有效）。

R代码

包络型：

library(Benchmarking)
x=matrix(c(2,2,5,10,10,3,12,8,5,4,6,12),ncol=2)
y=matrix(rep(1,6),ncol=1)
te=dea(x,y,RTS = "crs")##CCR模型的生产可能集是不变规模报酬（constant returns to scale)
rbind(te$eff,te$lambda)

线性模型：

library(Benchmarking)
x=matrix(c(2,2,5,10,10,3,12,8,5,4,6,12),ncol=2)
y=matrix(rep(1,6),ncol=1)
te=dea.dual(x,y,RTS = "crs")##CCR模型的生产可能集是不变规模报酬（constant returns to scale)
te$eff
te$u
te$v