阅读之前看这里👉：博主是一名正在学习数据类知识的学生，在每个领域我们都应当是学生的心态，也不应该拥有身份标签来限制自己学习的范围，所以博客记录的是在学习过程中一些总结，也希望和大家一起进步，在记录之时，未免存在很多疏漏和不全，如有问题，还请私聊博主指正。
博客地址：天阑之蓝的博客，学习过程中不免有困难和迷茫，希望大家都能在这学习的过程中肯定自己，超越自己，最终创造自己。

问题的提出

在深度学习的过程中，我们可能出现两种问题，一个问题是模型在训练集上表现不好，另一种问题是模型在测试集上表现不好(过拟合)。

针对这些问题，有什么可以优化的方法呢？

一、模型在测试集上表现不好的优化方法

1.激活函数的选择

神经网络的激活函数其实是将线性转化为非线性的一个函数，在深度学习中常用的激活函数有sigmoid function。

1.1 什么是Sigmoid function

一提起Sigmoid function可能大家的第一反应就是Logistic Regression。我们把一个sample扔进$sigmoid$中，就可以输出一个probability，也就是是这个sample属于第一类或第二类的概率。 还有像神经网络也有用到$sigmoid$，不过在那里叫activation function。Sigmoid function长下面这个样子：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$
其实这个function我们只知道怎么用它，但是不知道它是怎么来的，以及底层的含义是什么。

首先假设我们有两个class：C1和C2，并且给出一个sample $x$，我们的目标是求$x$属于C1的概率是多少。这个概率我们可以通过Naive Bayes很轻松的得出，也就是（公式1）：

其中等号右面的分布这项（公式2）：

$x$出现的概率等于C1出现的概率乘以C1中出现$x$的概率加上C2出现的概率乘以 C2 中出现 $x$的概率。 那么就可以把公式2带入公式1的分母中（公式3）：

下面我们将等式两边同时除以分子就变成了（公式4）：

也就是Sigmoid function

思考：
上面已经知道 sigmoid函数是从什么东西推导过来的了，那么有个问题就是，既然上面式子中只有 $P(x|C_1)$和 $P(x|C_2)$我们不知道，那我们干脆用Bayes不就能直接计算出$P(x|C_1)$了嘛？ （$x$是某个sample，其中有多个feature，也就是说x是一个vector）

但是Bayes有一个限制条件就是所有的feature都必须是independent的，假如我们训练的sample中各个feature都是independent的话，那么Bayes会给我们一个很好的结果。但实际情况下这是不太可能的，各个feature之间不可能是independent的，那么bias就会非常大，搞出的model就很烂。

1.2 这个$z$应该长什么样子

我们将$z$变换一下可以变换成下面的样子：

1.3 Sigmoid函数的好处

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。主要优点是平滑、易于求导。

sigmoid函数的导数是可以直接由自己来表示的，这在神经网络的反向传播的求导中起了大用途：

1.4 Sigmod函数的缺点（梯度消失和梯度爆炸的问题）

缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
对于梯度消失的问题：李宏毅老师视频中有这样两张PPT：

简单解释一下这上面的意思：
因为Sigmod函数的特性，在输入很大的情况，输出却变得很小，就算是增大输入，通过sigmoid函数得梯度也会变得很小，所以会造成学习速率很慢，也就是第一张图中的learn very slow。但是在靠近输出的地方，却学习很快。会造成一个现象就是：
当输入为random的时候，输出的地方已经根据这个random找到了一个局部最优值。

举个例子，对于一个含有三层隐藏层的简单神经网络来说，当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习。

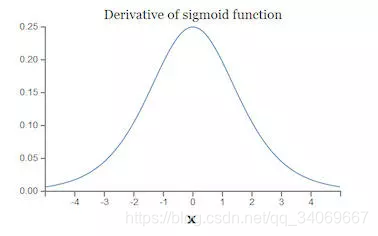
原因：当我们对Sigmoid函数求导时，得到其结果如下：

由此可以得到它Sigmoid函数图像，呈现一个驼峰状（很像高斯函数），从求导结果可以看出，Sigmoid导数的取值范围在0~0.25之间，而我们初始化的网络权值$|w|$通常都小于1，因此，当层数增多时，小于0的值不断相乘，最后就导致梯度消失的情况出现。同理，梯度爆炸的问题也就很明显了，就是当权值过大时，导致 ，最后大于1的值不断相乘，就会产生梯度爆炸。

从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。因此，梯度消失、爆炸，其根本原因在于反向传播训练法则，属于先天不足。如下图所示，对于四个隐层的网络来说，第四隐藏层比第一隐藏层的更新速度慢了两个数量级：

其它更多详细的内容可以看博客：

除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog